Dealing with "Things Unseen"

Science deals with unseen things like black holes by developing a testable hypothesis, which essentially describes what we would expect to see if there were black holes. When we observe behavior which matches the prediction, the hypothesis is confirmed. If not, it is rejected. Same for microwaves. When we observe behavior (thermal excitation of water molecules) consistent with energy transfer of microwaves, we confirm the theory! Religion on the other hand, takes an unexplained thing and blindly asserts #GodDidIt.  When the tests for god's existence fail, believers make up excuses for *why* it failed rather than reject the hypothesis. You're likely well aware of this method. The Bible provides many objective tests for the Christian god's existence, all of which demonstrably fail: - Matthew 7:7 “Ask, and it will be given to you seek, and you will find; knock, and it will be opened to you. - Matthew 21:22 And whatever you ask in prayer, you will receive, if you have faith.” - Mark 11:24 Therefore I tell you, whatever you ask in prayer, believe that you have received it, and it will be yours. - John 14:13-14 Whatever you ask in my name, this I will do, that the Father may be glorified in the Son. If you ask me anything in my name, I will do it So as a devout Christian, the first time you pray for something and it doesn't come true, you can know that the Bible is wrong. However, instead of admit their assumptions might be wrong, religious people blame themselves ("I must not have enough *faith*!") or make empty platitudes ("God works in mysterious ways.")

Geometry and a Flat Earth

We're told that the sun disappears over the horizon for the same reason that airplane contrails reach the horizon (which ironically is due to them following the curvature of the earth).  So let's consider perspective at night.  According to a Flat Earther I asked, Australia is about 10k miles from the US in a Flat Earth model.

We know that:

• $ \theta_{ele} = atan(h/d) $ Where h is the height of the sun off the flat earth and d is the distance to the sun's nadir point (directly below the sun). 
• When the sun is over Australia, it's dark in the united states.
• It's 10,000 miles from US to Australia.

Flat Earthers generally report that the sun is 3000 to 4000 miles in elevation. This is probably because if you tried to triangulate the sun (at approximately infinity miles away) from a curved surface you erroneously believed to be flat, you'd find that it appears to be about $ r $  miles away.

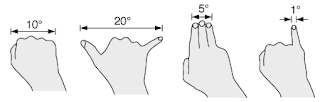
But how can that be?! $  atan(3000/10000) = 16.7  \degree $ !!. That's a pretty good elevation. About one and a half fists above the horizon! That would be pretty obvious! 

Making the small-angle approximation, these angles and distances scale approximately linearly.  To get as low as half of a fist above the horizon, we need 1/3 the height (let's say 1000 miles!). To get as low as one degree (still 2 sun widths) above the horizon, we'd need to be just 100 miles up. That's just at the edge of space. The sun could be hit with an amateyr  rocket!! 

With that, I've got no way to try to rescue this theory. The angles don't make sense.  Anyone got a way to make this problem work?

Collection of Satellite Images and Videos

I keep getting asked for pictures of satellites by #FlatEarthers I'm talking with. Rather than find them each time, here's a collection. The gif was from reddit.

Amateur Videos Showing Satellites

I'm not sure which satellites these are, but they're geostationary over Switzerland.  This sort of imaging is surprisingly easy to do (this guy does it VERY well!).  Just get a camera, a tripod, and take  5-10 sec exposures all night of the plane where the moon, sun, and planets pass.  Stitch them all together and you'll notice that some don't move.  Those are geostationary satellites.  You can figure out which ones they are with a bit of extra math.
Geostationary satellites in the Swiss Alps from Michael Kunze on Vimeo.

This guy wasn't even really trying, but when he co-adds frames (go make the streaking effect), it jumps right out.There's a clear GEO satellite near the top of the frame, about 40% in from  the left.

A Starry Night of Mt.Kilimanjaro from kwon, o chul on Vimeo.

This photographer isn't taking exposures long enough and has too much city light to see the satellites clearly. The "flashes" are likely glints off the solar panels or an aliasing artifact in his video conversion.  Longer exposures could cause streaking, but would bring the satellites out more clearly.
Geostationary Satellite Flashes, Night of March 7-8, 2013 from Ken Musgrave on Vimeo.

The folks at ExoAnalytic have some great professional videos through robotic telescopes.

Why not from other satellites?

I'm also often asked why we don't see satellites take pictures of other satellites.  To someone naive about otbits, this might seem like an easier task. You're closer, right? No. Space is very big, and satellites moving 17,000 mph, not all in the same direction!  Nevertheless, It's been done. An imaging satellite named Pléiades 1A took a picture of SPOT 5. 

Comparing Flat Earth Models to Reality

I finally found a video which helped me understand the flat-earther model of a sun circling a flat earth. Thanks to p-brain for helping me out here.

Setting aside his disastrous misunderstanding of perspective, he has a decent point regarding how distant points converge at long distances.  The "plane" that the sun would orbit within would indeed appear to approach (though never quite cross) the horizon.

I suspect this claim falls apart when we start examining distances necessary to accomplish this.  Clearly the Sun isn't flying along at 30,000 ft like the contrails p-brain uses as an example.  Rather, it would need to be flying a minimum of 2-3x higher. My intuition is that the angles will come closest to working if we set the sun at an altitude equal to the radius of the earth (4000 miles) .  

So let's compare the two approaches. For the sake of simplicity, I'll assume the curvature of the sun's path is so slight that we don't notice it curving northwards. That's right, I'm going to give the Flat  Earthers a pass on the fact that we don't see the sun curving to the north! No "Where's the curve?!" from me.  

So anyways, the distinction is really easy to make. If you believe in a Flat Earth, simply measure the angle to the sun throughout the day and compare the following plot of arctan(1/x): 

If it's straight, the angular rotation is constant, which matches the spherical earth model:

1. If the solar angle matches the plot of $ arctan(1/t) $, then it's a flat earth. 
2. If the solar angle is a straight line, it's a sphere.

Note: The angle you need to measure is called the "Right Ascension" (RA).  Align a pole to point to the North Star at night. Measure the angle to the sun about this pole.  This could be done with a protractor oriented perpendicular to the pole on the back side (away from the sun). Note the angle where the shadow is cast.  Here's my attempt to draw the experimental setup.