Geometry and a Flat Earth

We're told that the sun disappears over the horizon for the same reason that airplane contrails reach the horizon (which ironically is due to them following the curvature of the earth).  So let's consider perspective at night.  According to a Flat Earther I asked, Australia is about 10k miles from the US in a Flat Earth model.

We know that:

• $ \theta_{ele} = atan(h/d) $ Where h is the height of the sun off the flat earth and d is the distance to the sun's nadir point (directly below the sun). 
• When the sun is over Australia, it's dark in the united states.
• It's 10,000 miles from US to Australia.

Flat Earthers generally report that the sun is 3000 to 4000 miles in elevation. This is probably because if you tried to triangulate the sun (at approximately infinity miles away) from a curved surface you erroneously believed to be flat, you'd find that it appears to be about $ r $  miles away.

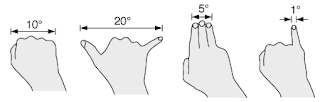
But how can that be?! $  atan(3000/10000) = 16.7  \degree $ !!. That's a pretty good elevation. About one and a half fists above the horizon! That would be pretty obvious! 

Making the small-angle approximation, these angles and distances scale approximately linearly.  To get as low as half of a fist above the horizon, we need 1/3 the height (let's say 1000 miles!). To get as low as one degree (still 2 sun widths) above the horizon, we'd need to be just 100 miles up. That's just at the edge of space. The sun could be hit with an amateyr  rocket!! 

With that, I've got no way to try to rescue this theory. The angles don't make sense.  Anyone got a way to make this problem work?